
An important class of continuous time LTI systems are those modeled by ordinary linear differential equations with constant coefficients.

Given an input x(t) and an output y(t),
![]()
is a linear first-order (the order of the derivatives is one) differential equation with constant coefficients (as long as a and b are constants).
A general nth order linear differential equation with constant coefficients is:
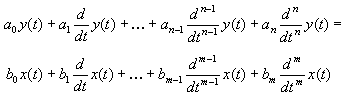
which we can write as:
![]()
A classical method for the solution of our differential equation is called the method of undetermined coefficients. We express the output y(t) as the sum of complementary or natural (yc(t)) and particular or forced (yp(t)) solutions:
y(t) = yc(t) + yp(t)
Natural response The natural response yc(t) is the solution to the homogeneous equation:
![]()
Assume that the solution of the homogeneous equation is:
yc(t)= Cest
Substituting in the homogeneous equation yields:
![]()
and we get:
![]()
This is the characteristic equation and it may be factored as:
![]()
The solution is of the form:
![]()
assuming there are no repeated roots (which is all we will cover here).
Ex. Given a first-order differential equation
![]()
find its homogeneous solution. Your answer should be in terms of a constant C.
Forced response The forced response yp(t) solves the equation
![]()
The form of the solution is determined by the input x(t). For an exponential input x(t)= A eat, the solution would be yp(t) = P eat where A, a, and P are constants.
Ex. For the previous example, assume an input x(t) = 6 e3 t. Find the particular solution yp(t).
Ex. Now, assuming that the system is initially at rest (the initial conditions are 0), i.e., y(0) = 0 , solve for the constant C in your overall solution y(t) = yc(t) + yp(t):
Ex. Given
y '(t) + 2y(t) = x(t)
where x(t) = 4 e2t, find y(t). Assume y(0) = 0.