Recall that the natural solution to our differential equation was:
![]()
where si is the root of the characteristic equation
![]()
The root of the characteristic equation si can be either real or complex. If it is complex, it must occur in conjugate pairs because the coefficients of the characteristic equation are real.
| • If si is complex, then | is exponential in form. |
| • If si is complex, then let | and | and the conjugate pair of these terms | ||
| can be expressed as: |
![]()
| where |
The roots si will determine if the overall system is BIBO stable.
Assume we have a causal LTI system. The solution to our differential equation is of the form
![]()
where y(t) = 0 for t < t0 (t0 is the start time). Since yp(t) is always of the same form as the input x(t), if the input x(t) is bounded, then yp(t) will also be bounded. (Alternatively, since we are only considering BIBO stability, our input is guaranteed to be stable.)
Thus, since the stability of the system will only depend on the system itself and not on the input, let's examine the solutions to the homogeneous equation:
![]()
Clearly, as long as the real part of all roots (also called poles) of this equation, σi < 0 (since we've assumed that the system is causal), then each term in yc(t) will be bounded. Thus, we require for BIBO stability that:
![]()
Thus, a necessary and sufficient condition for stability of a causal LTI system is that all roots of the system characteristic equation lie in the left half plane of the s-plane.
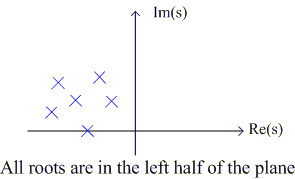
Ex. Given a causal LTI system described by the differential equation
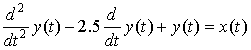
determine if the system is BIBO stable.
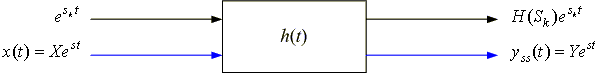
Given an input x(t) = X est to a BIBO stable LTI system modeled by an nth order linear differential equation with constant coefficients, we will examine the steady-state system response. Assume that X and s are complex.
The forced (particular or steady-state) response of the system to this input is of the same form of the input, i.e.
![]()
From the differential equation describing the system,
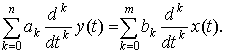
or,
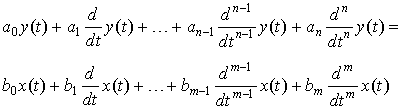
Plugging in x(t)= X est and yss(t)= Y est , we get
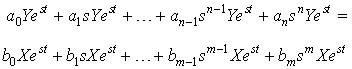
which we can write as Y = H(s) X
where
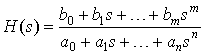
is a transfer function.
| So given an input | to an LTI system, the steady-state response is |
Similar to the differential equation and the impulse response, the transfer function H(s) completely characterizes the LTI system (we can derive the differential equation from H(s) and vice versa).
| In general, by superposition, given an input | 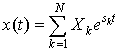 |
, the output of the system is |
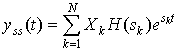 |
Eigenfunctions of CT LTI systems are complex exponentials:
![]()
Check: What is est*h(t)?
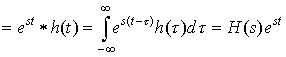
| where |  |
is the eigenvalue. This motivates the Laplace transform and the Fourier Transform: |
Ex.Given an input x(t) = est, and
h(t) = e3t u(t)
find its steady-state output
yss(t) = H(s) est
YOU FINISH: