In this section, we consider the analysis of stable LTI systems with periodic inputs. We will represent the input with a Fourier Series. We will consider the variation of the system response to frequency, i.e. the system frequency response.
| We saw that if we input a signal | to a stable LTI system, the steady-state response is |
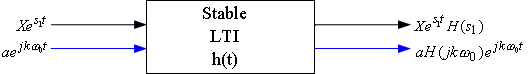
Next, if we input a periodic input signal (expressed with its Fourier Series) to a stable LTI system, using superposition, we can write down the output as a second Fourier Series:
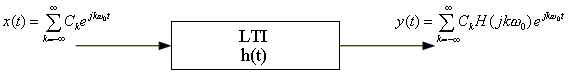
where
![]()
Note: y(t) is also a Fourier Series with Fourier Series coefficients CkH(jkω0). The book refers to the Fourier Series coefficients of x(t) as Ckx and those of y(t) as Cky. Notice that Cky = CkxH(jkω0).
Example Given an LTI system with impulse response h(t) = α e-αtu(t), α > 0.
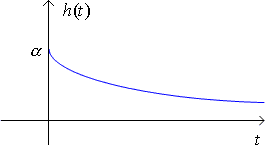
Find the output of the system to an input
x(t) = sin2(2t).
| HINT: First find | and then express x(t) as a Fourier Series. |
We will see that h(t) is a LOW PASS filter. If h(t) is used as a filter, it passes the LOW frequencies and cuts out the HIGH frequencies. In an image, examples of low frequencies are solid regions, while examples of high frequencies are edges.
Example Given a low pass filter in h(t) = e-tu(t) and an input signal
x1(t) = 1 + cos(t) + cos(8t)
find the output y(t).