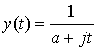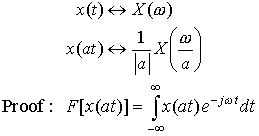
The point of this lesson is that knowledge of the properties of the Fourier Transform can save you a lot of work. We will cover some of the important Fourier Transform properties here.
Because the Fourier Transform is linear, we can write:
F[a x1(t) + bx2(t)] = aX1(ω) + bX2(ω)
where X1(ω) is the Fourier Transform of x1(t) and X2(ω) is the Fourier Transform of x2(t).
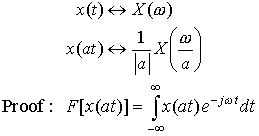
![]()
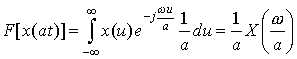
if a>0. If a< 0, then
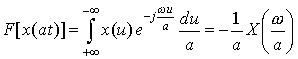
(since u=at). Therefore

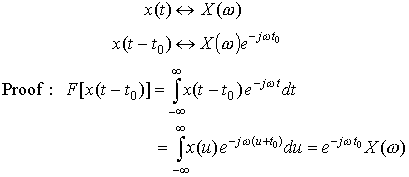
Note the DUALITY when you compare Examples 1 and 6 from Lesson 15.
Example 1 of Lesson 15 showed that the Fourier Transform of a block (or rect) function in time is a sinc in frequency. Example 6 of Lesson 15 showed that the Fourier Transform of a sinc function in time is a block (or rect) function in frequency.
In general, the Duality property is very useful because it can enable to solve Fourier Transforms that would be difficult to compute directly (such as taking the Fourier Transform of a sinc function). The Duality Property tells us that if x(t) has a Fourier Transform X(ω), then if we form a new function of time that has the functional form of the transform, X(t), it will have a Fourier Transform x(ω) that has the functional form of the original time function (but is a function of frequency). Mathematically, we can write:
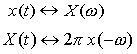
Notice that the second term in the last line is simply the Fourier Transform integral of the function X(t), i.e.
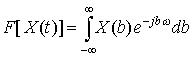
Therefore we get the Duality Property:
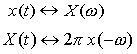
Example 1 Using the Fourier Transform integral equation, directly find the Fourier Transform of
x(t) = e-at u(t), a> 0
Example 2 Using the results of Example 1 and the Duality Property, find the Fourier Transform of