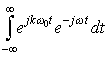
Example Find the Fourier Transform of the constant 1. Use duality and the fact that the transform of δ(t) is 1
We can also define a Fourier Transform for periodic signals. If a signal has both periodic and aperiodic components, then this will enable us to use one transform to deal with both the periodic and aperiodic components.
Can we take the Fourier Transform of a periodic signal? For example, we can write:
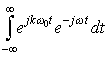
![]()
We can use either the Duality or Modulation Properties to show that:
![]()
We can check this by taking Inverse Fourier Transform (and using the sifting property):
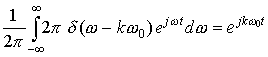
Now let's consider a general periodic signal x(t) that we can represent as a Fourier Series:
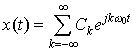
Since we know that:
![]()
by linearity of the Fourier Transform, we get that:
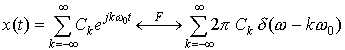
Thus we see that a periodic signal has a Fourier Transform that is an infinite impulse train at discrete frequencies kω0 with weights of 2πCk (many or most of the weights are usually 0).
Example Find the Fourier Transform of cos(ω0t).
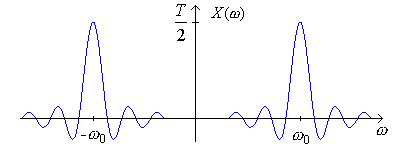
Example Find the Fourier Transform of the pulsed cosine:
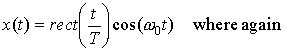

You can do it directly and also using the multiplication property.
Let's show this graphically: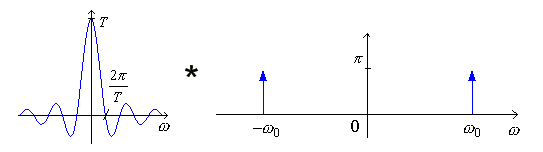
=