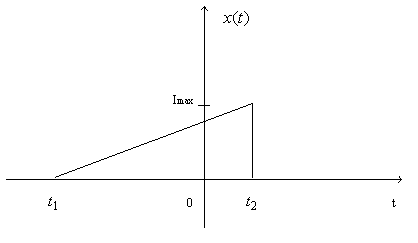
We reverse a signal x(t) by flipping it over the vertical-axis to form a new signal y(t) = x(-t).
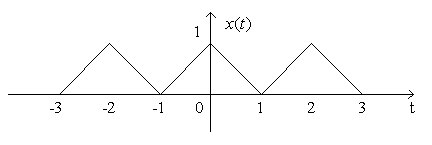
Example: Find
y(t) = x(-t)
where x(t) is:
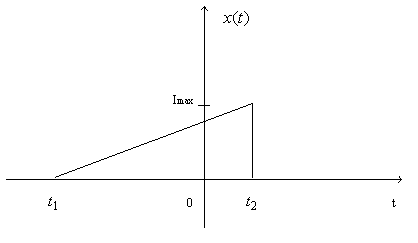
The signal y(t) = x(at) is a time-scaled version of x(t).
If |a| > 1, we are SPEEDING UP x(t) by a factor of a.
If |a| < 1, we are SLOWING DOWN x(t) by a factor of a.
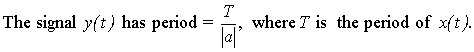
Example: Given x(t), find y(t) = x(2t). This SPEEDS UP x(t)
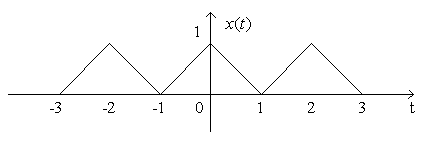
What happens to the period T?
The period of x(t) is 2 and the period of y(t) is 1, because
![]()
Example: Given x(t), find z(t) = x(t/2). This SLOWS DOWN x(t)
Example: Given y(t), find w(t) = y(3t) and v(t) = y(t/3).
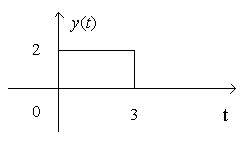
y(t) = x(t - t0)
Here, the original signal x(t) is shifted by an amount t0 .
Rule: set t - t0=0 and move the origin of x(t) to t0.
Given x(t) = u(t+2) - u(t-2), find x(t-t0) and x(t+t0).
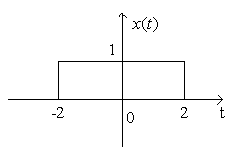
Example: Determine
x(t) + x(2-t)
where x(t) = u(t+1)- u(t-2)
Step 1: which of these functions is x(t)?
A, B, C or D
Step 2: Find x(2-t)
Method I to find x(2-t): Reverse in time, then delay.
Let y(t) = x(-t)
And y(t-2) = x(-(t-2)) = x(2-t)
Method II to find x(2-t): Advance, then reverse in time.
Let w(t) = x(t +2)
As the last step, add up x(t)and x(2 - t)
Combinations of Scale and Shift
Find x(2t+1) where x(t) is:
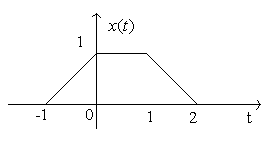
Method 1: Shift then scale: x(at+b):(i) v(t)=x(t+b); (ii) y(t) =v(at)= x(at+b).
|
v(t) |
= |
x(t+1) |
|
|
y(t) |
= |
v(2t) |
|
Method 2: Scale then shift: x(at + b) = x(a (t + b/a)) :
|
( i ) w(t) = x(at) ; |
|
( ii ) y(t) = w(t + b/a) = x(at+b) |
|
w(t) |
= |
x(2t) |
|
|
y(t) |
= |
w(t+1/2)) = x(2(t+1/2 )) = x(2t+1) |
|
Example: Given x1(t), find -x1(t), 2x1(t), and .5x1(t)
Example: Given x2(t), find 1 - x2(t). This is a case of adding together two signals.
Addition of two signals: x1(t) + x2(t)
To add two signals together, we simply add the values of the signals point-by-point.
Multiplication of two signals:x2(t)u(t)
To multiply two signals together, we simply multiply the values of the signals point-by-point.