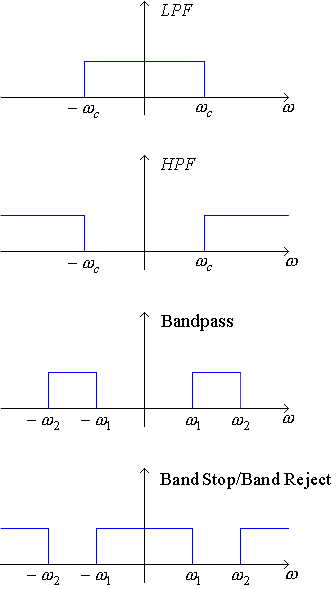
Given that an LTI system has the relationship y(t) = x(t) * h(t) where x(t) is the input, y(t) is the output, and h(t) is the impulse response of the system, we know that Y(ω) = X(ω) H(ω). H(ω) is a filter to eliminate unwanted parts of the frequency spectrum. There are a number of different types of filters including ideal low pass, high pass, band pass, and band stop, which are plotted here. These ideal filters have Fourier Transforms of the form rect(ω/2ωc), where ωc is the cutoff frequency. The corresponding time domain functions are sincs.

Example 1 Given two functions x1(t) = cos(500πt) and x2(t) = cos(1000πt), form a new signal x3(t) = x1(t) x2(t).
Draw the frequency response of a low pass filter that passes the low frequency component of the signal and blocks the high frequency component of the signal.
Modulation is multiplying a signal in time by complex exponentials (such as sine waves and cosine waves) to shift the signal to a desired frequency band. This is done, for example, by radio (or television) to assign different parts of the frequency spectrum to different radio (or television) stations. Remember that the Modulation Theorem told us that:
![]()
We will use the Modulation Theorem in an example of AM radio.
Example 2 AM radio - Double-sideband, suppressed carrier, amplitude modulation
Let x(t) be a music signal with Fourier Transform X(ω).
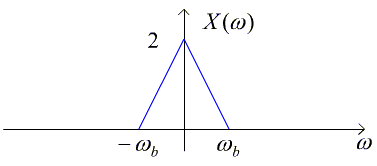
To modulate this signal, we'll form and transmit
y(t) = [x(t) + B] cos(ωct + φ)
where ωc is the carrier frequency of the radio station (e.g. 770 kHz), and B is the carrier. Let B=0 which means that we have a suppressed carrier and let φ = 0 for simplification. In this case, y(t) = x(t) cos(ωct).
Then
![]()
Now, let's look at the Fourier Transform of the modulated signal y(t). Y(ω) = ?
Your radio demodulates the signal by multiplying the received signal y(t) by another cosine wave to form a third signal z(t):
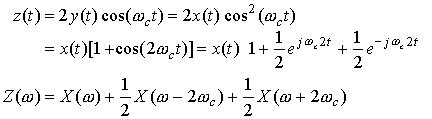
To recover the original music signal x(t) from the demodulated signal z(t), you filter z(t) with a low-pass filter by multiplying by a rect function in frequency. This corresponds to convolving with a sinc function in time.