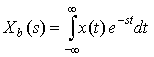
In this lesson, we cover the Bilateral Laplace Transform. We will see that for the Bilateral Laplace Transform we must specify Region of Convergence (ROC) because multiple signals have the same Laplace Transform. The Bilateral Laplace Transform is defined as:
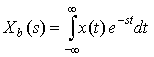
Example 1
Example 2
Notice that the Laplace Transforms for Examples 1 and 2 were the same, except that they had different Regions of Convergence. Therefore, we must always specify the ROC when working with the Bilateral Laplace Transform so that we can determine whether the time signal is left-sided or right-sided.
We state without proof here that the ROC of the Laplace Transform of the sum of multiple time functions is the INTERSECTION of the individuals ROCs. Use this fact to solve the next two Examples.
Example 3
Example 4
To compute the Inverse Bilateral Laplace Transform, we'll again use Partial Fraction Expansion. We will ignore the case of multiple poles. Write the Bilateral Laplace Transform H(s) as:
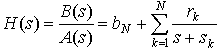
Here, sk are the poles, rk are the residues, and bN is nonzero if the order of the numerator B(s) is greater than the order of the denominator A(s).
Example 5
Example 6
Example 7
Remember, you can always check your results of taking the inverse transform by taking the transform and comparing.