(x(t) + x(-t))
(x(t) - x(-t))
Any continuous time signal can be expressed as the sum of an even signal and an odd signal:
x(t) = xe(t) + xo(t)
| Even : xe(t) | = | xe (-t) |
| Odd: xo(t) | = | -xo(-t) |
An even signal is symmetric across the
vertical axis.
An odd signal is anti-symmetric across the vertical axis.
| xe(t) | = |
|
(x(t) + x(-t)) |
| xo(t) | = |
|
(x(t) - x(-t)) |
Example, given the unit step function (a discontinuous continuous-time signal),

find ue(t) and uo(t)
How can we tell if a continuous- time signal x(t) is periodic? That is, given t and T, is there some period T >0 such that
x(t) = x(t + T)?
If x(t) is periodic with period T, it is also periodic with period nT, that is:
x(t) = x(t + nT).
The minimum value of T that satisfies x(t) = x(t + T) is called the fundamental period of the signal and we denote it as T0.
The fundamental frequency of the signal in hertz (cycles/second) is
![]()
and in radians/second, it is
![]()
If x1(t) is periodic with period T1 and x2(t) is periodic with period T2, then the sum of the two signals x1(t) + x2(t) is periodic with period equal to the least common multiple(T1, T2) if the ratio of the two periods is a rational number, i.e.:
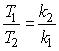
Let T ' = k1T1 = k2T2, and z(t) = x1(t) + x2(t),
z(t + T ' ) = x1(t + k1T1) + x2(t + k2T2) = x1(t) + x2(t) = z(t)
Examples of periodic signals are infinite sine and cosine waves.
Examples: Given x1(t) = cos(3t), and
x2(t) = sin(5t).
find the period of x1(t)+
x2(t) or state that it is aperiodic.
Examples: Given
x1(t) = cos(6t), and x2(t) = sin(8t).
find the period of x1(t)+
x2(t) or state that it is aperiodic.
Examples: Given
x1(t) = cos(t), and x2(t) = sin(πt).
find the period of x1(t)+
x2(t) or state that it is aperiodic.
x(t) = C eat, C and a can be complex.
a = σ + jω0, σ = real part, ω0 = imaginary part.
These are very important because complex exponential are "eigenfunctions" of LTI systems:
As we will see, if you input x(t) = eat to a linear time-invariant system, we will get y(t) = H(a)eat as the output.

*** EULER's FORMULA *** - Memorize:
ejθ = cosθ + jsinθ
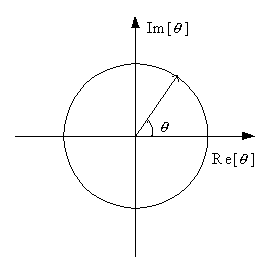
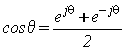
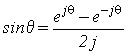
1.) Case 1, C and a real, x(t) = Ceat
• a = σ > 0.
GROWING exponential,
Chemical reactions, uninhibited growth of bacteria (as might
be found if the potato salad is left out too long), human population
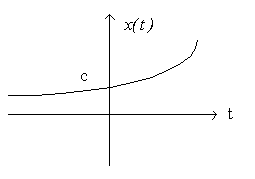
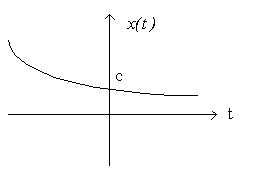
• a = σ < 0.
DECAYING exponential
Radioactive decay, RC circuit response, damped ME system.
• a = σ = 0 => x(t) is constant (DC) signal.
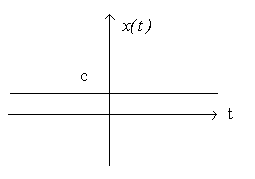
2.) Case 2, C complex, and a
imaginary,
a is purely imaginary (σ = 0),
a = jω0
C = Aejφ where A and φ are
real
![]()
x(t) is a complex sinusoid.
If C is real (φ=0), then
x(t) = Acosω0t + jAsinω0t.
In both cases, x(t) is periodic, i.e.
x(t) = x(t + T) where T is the period.
Why is x(t) periodic?
x(t) |
= |
|
|
x(t + T) |
= |
|
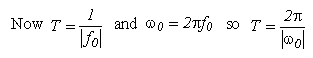
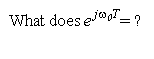
A real sinusoid:

T is the fundamental period
3.) Case 3
In the most general case, C and a are complex:
|
C |
= |
|
|
x(t) |
= |
|
|
= |
|
|
|
= |
|
|
|
= |
|
The real part is Aeσtcos(ω0t + φ)
The imaginary part is Aeσtsin(ω0t + φ)
Example: Plot real part of this signal for σ > 0 and σ < 0
|
|