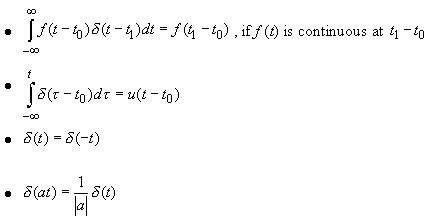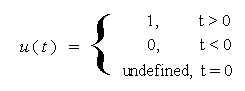
We already defined the unit step function u(t) as:

Ex: Find and plot u(t - t0) and u(t - t1)
Ex. Define a block function (window) as
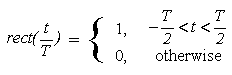
|
Then |
|
Example: Plot |
Now let's look at a signal: |
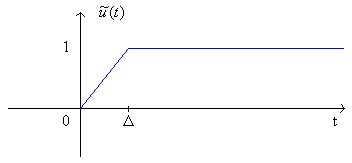
What is its derivative? Define it as:
![]()
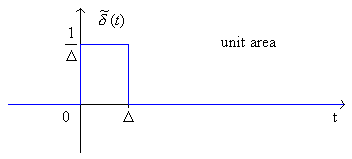
which has unit area.
Now, |
So what if we take |
? |
The pulse height gets higher and higher and its width goes to 0, but its area is still 1!
So define δ(t) as the unit impulse:

AND

or equivalently,
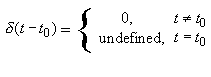
AND
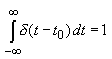
Also,
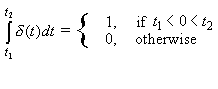
δ(t) can be considered to be the derivative of u(t) but only in a restricted sense since u(t) is a discontinuous function.
Note that the impulse function is not a true function since it is not defined for all values of t. It's a "generalized function." But its idealization will allow us to derive many interesting results.
1. Scaling
Kδ(t) is an impulse with weight or area K:
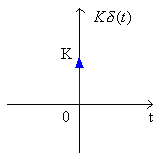
2. Multiplication of a function x(t) (that is continuous at 0) by an impulse δ(t):
We get an impulse with area or weight x(0).
3. Time Shift of an impulse
y(t) = x(t)δ(t-t0)
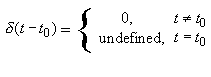
So we get an impulse with weight equal to the value of x(t) where the impulse is located:
y(t) = x(t0)δ(t-t0)
Example What is Kx(t)δ(t-t0)?
Example What is 3u(t-1)δ(t) ?
***SIFTING PROPERTY***
What if we multiply a function by an impulse and then integrate?
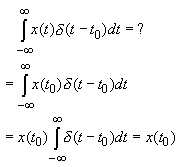
We integrate out the time variable so the integral is just equal to a number (or later on, a function). We'll see this many times.In this case, the impulse δ(t-t0) is defined by the integral (as long as the function x(t) is continuous at t0).
Ex.
ALSO: