
A SYSTEM is an operation for which cause-and-effect relations exist.

Here, we discuss some of the properties that a continuous-time system could have. We will use x(t) for the input to the system, y(t) as its output, and use the notation:
y(t) = T[x(t)]
or
y(t) = S[x(t)]
or
x(t) → y(t)
Systems whose output
y(t0) at time
t0 depends on values of the input other than just
x(t0) have memory.
In other words, a system y(t0) has memory if its output at time t0 depends on
the input x(t) for t > t0 or t < t0,
i.e. it depends on values of the input other than x(t0).
Otherwise, the system is MEMORYLESS
Example of a memoryless system:
Resistor v(t0) = R i(t0); the voltage at time t0 depends only on the current at time t0.
Example of System with Memory:
|
Capacitor |
; the voltage depends on past values of the current so a capacitor has memory. |
Ex 1. Does y(t) = x(t)
+ 5 have memory?
Ex 2. Does z(t) = x(t + 5) have memory?
Ex 3. Does y(t) = (t + 5)x(t) have memory?
Ex 4. Does z(t) = [x(t + 5)]2 have memory?
Ex 5. Does a(t) = x(5) have memory?
Ex 6. Does v(t) = x(2t) have memory?
A system is invertible if you can determine the input uniquely from the output, i.e. there is a one-to-one relationship between the input and output. In this case, we would write that the inverse of the system S is SI:
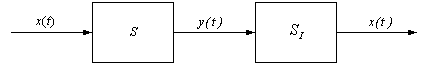
A resistor is invertible because you can recover the current from the voltage: x(t) = i(t) , y(t) = v(t), x(t) = y(t)/R.
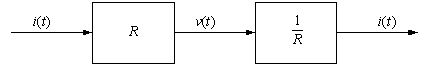
y(t) = x5(t) is an invertible system since it is one-to-one.
Examples of some systems that are not invertible:
y(t) = x(t)u(t)
→ zeros out much of the input
y(t) = x2(t) → don't know sign
y(t) = cos[x(t)] → add 2π to
x(t)
Output y(t) depends only on past and present inputs and not on the future.
All physical real-time systems are causal because we can not anticipate the future. Clearly, the stock market is a causal system.
Physical systems that are noncausal are not real-time. For example, a system in which music is recorded and processed later is noncausal but it is not real-time
If a system is memoryless, it is also causal. However, being causal does not necessarily imply that a system is memoryless. In fact, most causal systems do have memory.
Examples: Resistors and capacitors are causal systems:

| Ex 7. |
Is this Causal? You fill in.
Ex 8. Let y(t) = x(-t).
Is this causal? Try letting t be a negative number.
We will consider Bounded Input - Bounded Output (BIBO) Stability
We say that a system is BIBO stable if an input x(t) that is bounded (finite) for all time produces an output y(t) that is also bounded or finite for all time.
Mathematically,
we write if |x(t)|
![]() B1 →
|y(t)|
B1 →
|y(t)| ![]() B2, where
B1 and B2 are finite constants and
y(t) is the output.
B2, where
B1 and B2 are finite constants and
y(t) is the output.
In this example, the input x(t) is bounded by the constant B1 and the output y(t) is bounded by a second constant B2:
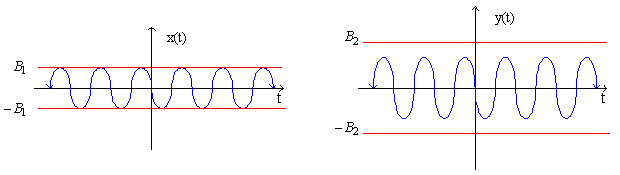
Example 9: A resistor is stable because:
If | i(t) | ![]() B1 → | v(t) |
B1 → | v(t) |
![]() RB1
RB1
| Example: 10 | Capacitor: |
Is this stable?
Let i(t) = B1u(t), where B1≠0
| grows linearly with t and as | , | . So a capacitor is not BIBO stable. |