Linearity

For a system to be linear, it must satisfy both the additivity and homogeneity properties:

  1. Additivity

    If S[x1(t)]  = y1(t) and S[x2(t)]  = y2(t) → S[x1(t) + x2(t)]  = y1(t) + y2(t) means that a system satisfies the additivity property.

  2. Homogeneity or Scaling

    S[x(t)]  = y(t) → S[ax(t)]  = ay(t) means that a system satisfies the scaling or homogeneity property.

Combine Additivity and Homogeneity to get the SUPERPOSITION CONDITION:

If S[x1(t)]  = y1(t)  and  S[x2(t)]  = y2(t)
then S[ax1(t) + bx2(t)]  = ay1(t) + by2(t)

Examples of Linear systems

Multiplication by a constant:

S[x(t)] = cx(t)

Try: S[ax1(t) + bx2 (t) ]:


S[x1(t)]  =   cx1(t)  =  y1(t)
S[x2(t)]  =   cx2(t)  =  y2(t)
S[ax1(t) + bx2 (t) ]

  = 

   acx1(t)  +  bcx2(t)
 = 

  ay1(t)  +  by2(t)

Therefore, linearly combined input produces linearly combined output and the system is linear.

Examples of Nonlinear systems

  1. 1) Squaring

    S[x(t)]  = y(t) =  x2(t)

    Violates homogeneity,

    S[x(t)]  =   x2(t)
    S[ax(t)]  =   a2x2(t) ≠  ax2(t)

    (It also violates Additivity due to the cross-terms.)

  2. 2) Affine or Incrementally linear system

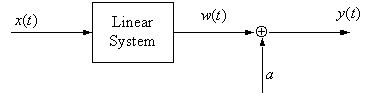
    S[x(t)]  =  y(t)  =   x(t) + a

    This system violates homogeneity:

    S[x(t)]  =   x(t) + a
    S[cx(t)]  =    cx(t) + a ≠  c[x(t) + a]

    It also violates additivity:

    S[x1(t)]  =   x1(t) + a
    S[x2(t)]

    		  =   x2(t) + a
    S[x1(t) + x2(t)]  =   x1(t) + x2(t) + a   ≠  S[x1(t)] + S[x2(t)]

    But we can think of this as a system that is "incrementally linear" or affine (note that the first part of the system is linear):

Note: If the input to a linear system is zero, the output will also be zero. Use the scaling property to show this:

S[x(t)]  =  y(t) → S[ax(t)]  =  ay(t)

If we let a = 0, then we get that S[0] = 0.
For an affine (nonlinear) system such as

S[x(t)] =x(t) + 3

A zero input produces non-zero output, i.e. S[0]=3. This violates the requirement that a linear system produce a zero output to a zero input.

Superposition:

We can generalize superposition to more than 2 functions, i.e. given a set of inputs xk(t) with a set of corresponding outputs yk(t), we can take a linear combination of any number of the inputs and get the same linear combination of the corresponding outputs:

You will find this very useful in doing some convolutions.

Are the following systems linear?


  1. y(t) = tx(2t)



  3. y(t) = cos[x(t)]



  5. y(t) = |x(t)|