In this lesson, we will discuss linear time-invariant (LTI) systems - these are systems that are both linear and time-invariant. We will see that an LTI system has an input- output relationship described by a convolution.
Using the sifting property, we can write a signal x(t) as:
![]()
which is writing a general signal x(t) as a function of an impulse function. This expresses the input x(t) as an integral (continuum sum) of shifted impulses that are weighted by weights x(τ). Another way to put this is that you can build a CT signal out of impulses.
We can write:

This expresses the input x(t) as an integral (continuum sum) of shifted impulses that are weighted by weights x(τ).
Now take a system and define the impulse response of the system as

h(t) = S[δ(t)]
and the response of the system to a shifted impulse as:

h(t,τ) = S[δ(t - τ)]
If the system is linear, then

S[αx1(t) + βx2(t)] = αy1(t) + βy2(t)
Let

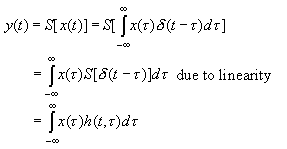
But what if the system is also Time-Invariant?
Then S[δ(t - τ)] = h(t , τ) = h(t - τ), since we had S[δ(t)] = h(t). Therefore,
![]()
We have seen that if we have a linear time-invariant system, then the output is the input convolved with the system's impulse response h(t). In other words, we can completely characterize an LTI system by its impulse response.
This is a very important result!

Convolution Integral:
![]()
Here, h(τ) is flipped and shifted across x(τ).
Convolution is a tough concept to get at first. I have 2 rules that will greatly improve the quality of your life:
Why can we pick which function to flip?
Because convolution is commutative:
![]()
Change variables: λ = t - τ → τ = t - λ, dτ = -dλ.
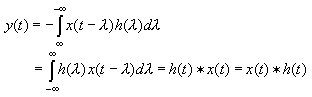
(minus signs cancel)
Let's examine convolution formula:
![]()
Fortunately, it usually falls out that there are only several regions of interest and the rest of y(t) is zero.
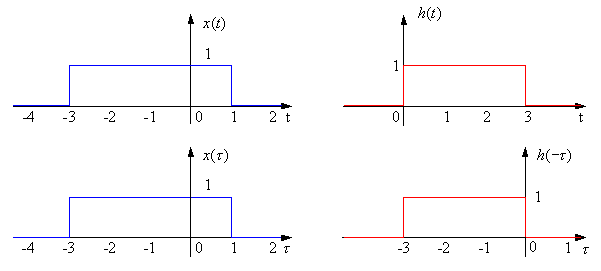
Ex. Find y(t) = x(t)*h(t).
Form x(τ) and h(t - τ) (to shift by h(- τ) by t, just add t to all points) and continue from there.

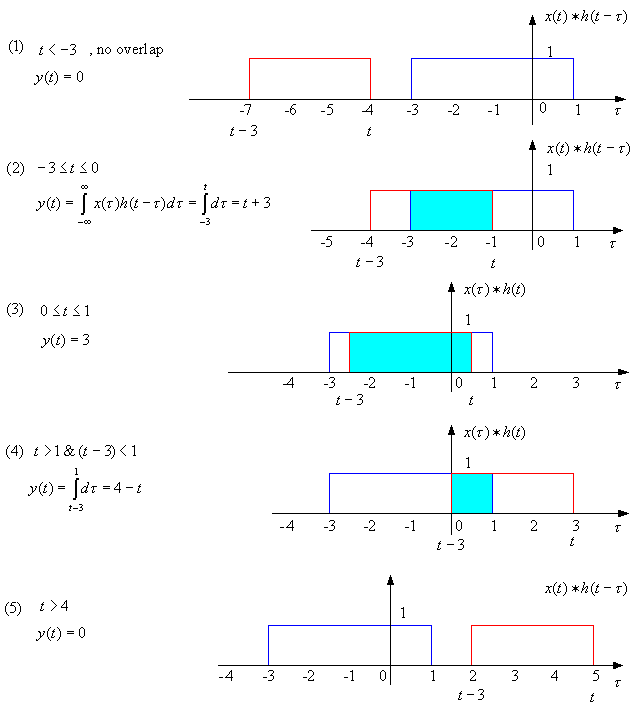
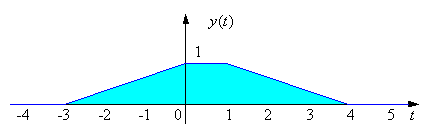
When you finish notice: