The Step Response is the response of an LTI system to a unit step function. In other words, the input to the system is simply the unit step function: x(t) = u(t).
This is equivalent to simply integrating the input from the infinite past up to time t.
![]()
Example 1
Superposition (or Divide-and-Conquer):
We can directly apply superposition to find the output of LTI systems if x(t) can be expressed as a linear combination of basis functions Φk(t).
The Φk(t) are some convenient set of functions, for example unit impulses, unit step functions, or complex exponentials.
| Example 2 If an input is written as:
|
![]()
using superposition, we can write its output as:
![]()
where
Ψk(t) = S[Φk(t)] = h(t) * Φk(t) = Φk(t) * h(t)
Again, using superposition, we can write:
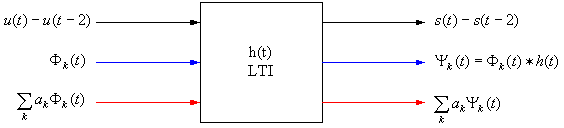
Example 3
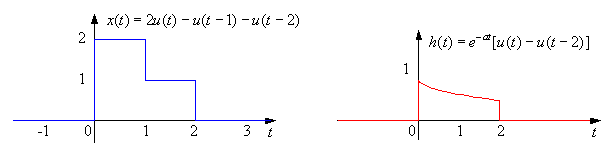
Find the output of the system where
x(t) = 2u(t) - u(t - 1) -
u(t - 2) and
h(t) = e-at [ u(t) - u(t - 2) ].
Convolution is commutative, associative, and distributive. Keeping this in mind may simplify some convolutions for you.
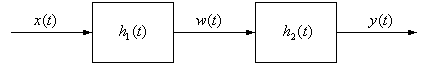
w(t) = x(t) * h1(t), y(t) = w(t) * h2(t)
= [ x(t) * h1(t) ] * h2(t)
= x(t) * [h1(t) * h2(t)], by associativity of convolution
Therefore the impulse response h(t) for this overall system is h1(t) * h2(t).
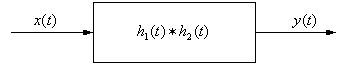
We can change the order in which the convolutions are performed due to commutativity. For a cascade of M systems there are M! possible system orderings.
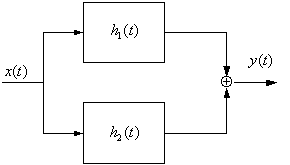
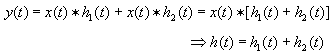
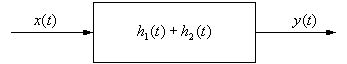
Parallel systems is a large area of research today.