We saw that input/output properties of an LTI system are completely determined by the system's impulse response h(t). We also saw that the output y(t) = x(t) * h(t), that is, the output of the system is simply the convolution of the input with the system's impulse response.
In this section, we will express other known system attributes in terms of conditions on the impulse response h(t).
In a memoryless system, the output y(t) is a function of the input x(t) at the time instant t alone. It does not depend on either past or future inputs.
An LTI system that is memoryless can only have this form:
y(t) = x(t) * h(t) = Kx(t)
Here, K is the system gain and it must be constant or else the system would vary with time.
For y(t)= Kx(t), the impulse response h(t) must be of the form of a unit impulse weighted by a constant K:
h(t) = Kδ(t)
Example 1
Is a system with impulse response
h(t) = Kδ(t - d), d ≠ 0? memoryless?
Example 2 Is a system described by h(t) = u(t) - u(t - 1) memoryless?
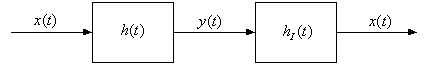
h(t) * hI(t) = δ(t)
A system is invertible if we can find hI(t) so that the original input x(t) can be recovered from the output y(t). For this to hold, the system must be one-to-one.
We will see how to do this when we study transforms.
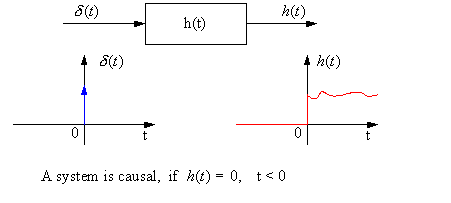
We know that for a causal system, the output depends only on past or present inputs and not on future inputs.
Equivalently, a causal system does not respond to an input until it occurs (the output is not based on the future).
In other words, a response to an input at t = t0, would occur only for t 
t0 and not before t0.
We know that h(t) is the system response to δ(t), and that δ(t) occurs at t = 0.
Another way to look at the causality condition: Let's examine the convolution equation, flipping h(t) instead of x(t):
Causality: if h(t) is causal then h(t - τ) = 0, t - τ < 0 or t < τ.
So,
which shows us that the output y(t) depends only on values of the input x(τ) for
τ 
t, i.e. it only depends on the past and present.
Example 3
Is h1(t) = u(t + 1) causal?
Is h2(t) = u(t - 1) causal?
We can tell if an LTI system is BIBO stable from its impulse response.
|x(t)|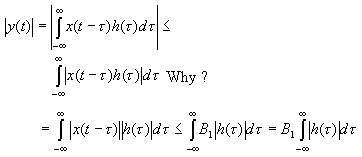
B1, for all t, to determine if the
system is BIBO stable, we need to determine if its output remains bounded for all time:
That is, the system is BIBO stable iff the impulse response h(t) is absolutely integrable:
In this case, the output will be bounded
by a second constant:
|y(t)|
B1G = B2 and
thus, the system is BIBO stable.
Example 4 Is h(t) = u(t) stable?
(This just gives the running integral of x(t).)
Example 5 Given an impulse response h(t) = e-atu(t), a > 0, is the system BIBO stable? How about for a < 0?
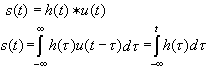
We see that the step response s(t) is just the running integral of the impulse response h(t).
Thus, we can recover the impulse response h(t) from the step response s(t) by taking its derivative:
Example 6 Given a step response
find the system's impulse response h(t) by taking the derivative of s(t)