













| 9.3 Phasor (10) |
 |
 |
 |
 |
|
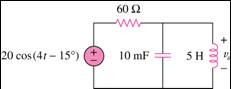
| • | In-class
exercise for Unit 6a, we can derive the differential |
|||
| equations for
the following circuit in order to solve for vo(t) |
||||
| in phase domain
Vo. |
||||
 |
 |
|
| • | However, the
derivation may sometimes be very tedious. |
|
| Is there
any quicker and more systematic methods to do it? |