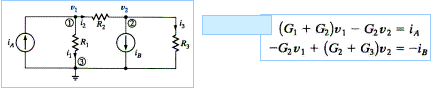
THE CONVENTIONAL
ANALYSIS USING MATHEMATICAL MODELS REQUIRES THE DETERMINATION
OF (A SET OF) EQUATIONS
THAT REPRESENT THE CIRCUIT.
ONCE THE MODEL IS
OBTAINED ANALYSIS REQUIRES THE SOLUTION OF THE EQUATIONS FOR
THE CASES REQUIRED.

ANALYSIS OF LINEAR CIRCUITS WITH INDUCTORS AND/OR CAPACITORS