Inductors and Capacitors, Part II
This article describes the basics of capacitance and inductance. An
understanding of calculus is helpful, but not necessary. A basic understanding
of voltage and current is assumed. This article uses a higher level of
mathematics than most of the tutorials. A knowledge of complex arithmatic is
also helpful.
Complex Numbers
Complex numbers are those that involve the square root of -1. Since a square
root can never be negative (it doesn't matter if the number is positive or
negative, if you square it you end up with a positive number), this is called an
imaginary number. At first you might think that dealing with an imaginary number
is just another excuse for those mathematical type persons to go off and fill a
page with useless equations. However, it turns out that these imaginary numbers
have properties that make them very useful in electronics.
In mathematics, the square root of -1 is usually written using a lower case
letter i. In electronics, i stands for current (intensity), so we use j for the
square root of -1 instead.
Complex numbers have two parts. The first is the real term, which is the type
of number we are used to dealing with on a daily basis. The second part is the
imaginary term, which is a multiple of j. Either term may be zero.
Reactance and Complex Numbers
The reactance of a capacitor (Xc) is given by the formula Xc=1/(jwC), where C
is the capacitance and w=2(pi)f (and f is the frequency). The w is usually
written as a greek omega, but hey, this is only an ASCII text, so we have to
make do with a w. Note that the reactance changes with the frequency, just as
the current vs. voltage changed with the frequency in part I of this article.
The inductive reactance (Xl) equals jwL, where L is the inductance, and
w=2(pi)f. Note that the reactance of capacitors and inductors both contain no
real terms.
You can think of the reactance as being somewhat equivalent to the
resistance.
Phasors
Sorry, we aren't talking about Star Trek here. A Phasor is simply a complex
number. If you use the real and imaginary numbers as x and y values on a graph,
you can plot complex voltages, currents, impedences, etc. as vectors. This is a
little complicated, but hopefully using impedence as an example will make it
more clear.
Impedence is simply how much the electricity is impeded, or restrained. For a
simple resistor, the impedence was the resistance. For a capacitor or inductor,
the impedence is the reactance. Impedence is, in general, a complex number. It
contains a real part and an imaginary part. The real part comes from real
resistance. The imaginary part comes from reactance. This is easy to remember,
since inductors and capacitors don't absorb energy like a resistor (which
converts the energy into heat). Instead, inductors and capacitors store and
release energy.
We usually use a capital Z to represent impedence. Since it has a real and an
imaginary component, Z=R+X. Now, here's the fun part. Remember Ohm's Law? Well,
we can still use it, even with capacitors and inductors (this is the beauty of
phasors, we can use simple algebra and phasors to solve problems instead of
being forced to use calculus).
We usually use a capital V and I to represent voltage and current as phasors.
The formula is simply V=IZ (very similar to V=IR for resistors), only now we are
using phasors instead of simple real numbers.
As an example, let's assume we have a 150 ohm resistor, a 2 mH inductor, and
a 473 uF capacitor all in series, connected to a voltage source of 120 volts AC,
60 Hz. The total impedence is Z=R+Xl+Xc, or Z=150+jw(.002)+1/(jw(.000473)), and
w=2(pi)(60), or 120(pi). One important thing to note here is that 1/j is equal
to -j. If this doesn't make sense, consider what happens if you multply the top
and bottom both by j. You end up with j/(j squared), and (j squared) is negative
one, and j/(-1) equals -j. If we continue solving for Z, we get
Z=150+0.75j-5.61j (approximately), or Z=150-4.86j. Note that we just added up
all of the impedences, the same way we did for resistors in series.
To solve for the current, it is easiest to use the polar notation for the
phasor. If you graph the real and imaginary terms as vectors, you end up with a
resultant vector. 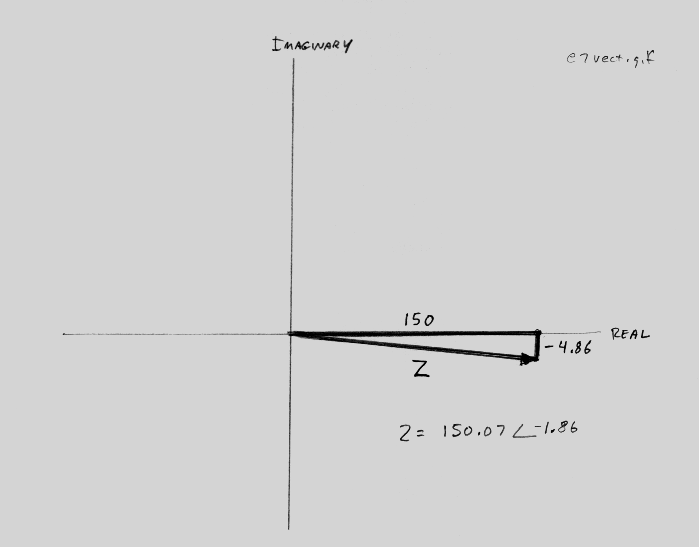 This
vector has a magnitude and a direction. The magnitude is the square root of R
squared plus X squared (where R and X are the real and imaginary parts), and the
angle, usually written as a greek theta, is the inverse tangent of (X/R). We
write this as (magnitude)<(angle), where the < is really an angle sign. If
you are writing it by hand, you make it look more like an angle than a less than
sign. Some people continue the bottom of the line under the angle value, so that
it cannot be mistaken for a less than sign.
This
vector has a magnitude and a direction. The magnitude is the square root of R
squared plus X squared (where R and X are the real and imaginary parts), and the
angle, usually written as a greek theta, is the inverse tangent of (X/R). We
write this as (magnitude)<(angle), where the < is really an angle sign. If
you are writing it by hand, you make it look more like an angle than a less than
sign. Some people continue the bottom of the line under the angle value, so that
it cannot be mistaken for a less than sign.
In our example, the magnitude is 150.07 and the angle is -1.86. If we write Z
in polar form, it is then 150.07<-1.86.
Ok, now we are ready to find the current. The formula is V=IZ. We know Z and
V, so we need to solve for I. If we rearrange the formula, we get I=V/Z, or I =
(120<0)/(150.07<-1.86). To divide the phasors, we simply divide the
magnitude and subtract the angle. So, I=(120/150.07)<(0-(-1.86)), or
0.800<1.86.
We can convert this back to rectangular form (using the real and imaginary
terms) very easily. The real part is (magnitude)cos(angle), and the imaginary
part is (magnitude)sin(angle). I is therefore 0.8cos(1.86)+0.8sin(1.86)j, or
0.800+0.026j.
Note that the angle (called the phase angle) of the current is greater than
the angle of the voltage (which was zero). This means that the current is
leading the voltage. Current in capacitive circuits leads the voltage, and lags
behind the voltage in inductive circuits.
Summary of Phasors
The use of phasors can be a little confusing at first, but it is a valuable
technique for solving circuits, especially in power line circuits where the
frequency is a constant. In other circuits, plotting a few values may give you a
good idea of how the circuit is operating at different frequencies. Remember
that all signals can be broken down into a sum of various sine waves, so that
looking at the response of individual frequencies can let you see how the
circuit will perform for any arbitrary waveform.
The use of phasors requires conversions between polar and rectangular forms,
but otherwise lets you use simple algebra to solve the equations. This allows us
to use the simple V=IZ and P=VI formulas, instead of being forced to deal with
things like i=C(dv/dt). 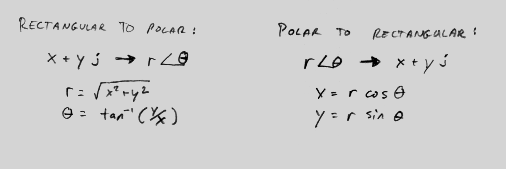 To multiply two phasors together (in polar form), multiply the magnetudes and
add the angles. To divide, divide the magnitude and subtract the angles.
Addition and subtraction are more easily done in rectangular form. Just
add/subtract all of the real terms as neccessary, and then add/subtract all of
the imaginary terms.
To multiply two phasors together (in polar form), multiply the magnetudes and
add the angles. To divide, divide the magnitude and subtract the angles.
Addition and subtraction are more easily done in rectangular form. Just
add/subtract all of the real terms as neccessary, and then add/subtract all of
the imaginary terms.
Watts and Vars
If you deal with computer uninterruptable power supplies, you know that they
are rated in volt-amps instead of watts. What is a volt-amp, you ask? Well,
quite simply it is the volts multiplied by the amps. From the above discussion
on phasors, you should now realize that this may result in a complex number (for
a computer UPS, all they give you is the magnitude in the specs). If you convert
this into a real and an imaginary component, the real part is called the watts,
and the imaginary part is called the vars (var = volt amp reactive).
You may also encounter a term called the power factor. The power factor is
the cosine of the current angle subtracted from the voltage angle. A power
factor of 1 means that the voltage and current are perfectly in phase. The power
company likes to have a power factor of 1 on their lines, since this makes the
transmission of power more efficient. Since most household loads are slightly
inductive (due to motors in hair dryers, vacuum cleaners, dishwashers, etc), the
power company adds capacitors to the line to compensate for the inductance.
Frequency Effects and Practical Applications
Capacitors and inductors are usually used in circuits which take advantage of
the fact that their response varies with frequency. One use is power supply
filters. If you put a capacitor in parallel with your load across the terminals
of the power supply, as the frequency gets higher, the reactance of the
capacitor gets smaller. At higher frequencies, the capacitor effectively
provides a short circuit across the power supply, but at DC, the reactance is
extremely large, so large that the capacitor does not seem to even exist in the
circuit. When capacitors are used in this way, they are called bypass
capacitors, since they bypass the power supply.
Remember from the formula Xc=1/(jwC) that the reactance gets smaller as C
gets larger. Therefore, larger capacitors work better as power supply bypass
capacitors. You will often see large electrolytics used as the main filter
capacitors in a power supply. However, since electrolytics do not function
properly at higher frequencies, you will also often see smaller ceramic disc
capacitors in parallel with the electrolytics. These capacitors work well at
higher frequencies, and function to get rid of the noise that the electrolytics
would not filter off. In many circuits, especially higher frequency digital
circuits, individual chips will have a small ceramic capacitor (typically 0.1
uF) bypassing the power leads. This capacitor is installed physically very close
to the chip and care is taken to keep the signal path very short from the
capacitor to the chip. This allows the capacitor to filter off any high
frequency noise that might be present, and helps to keep the chip operating more
reliably. Op amps will often oscillate or do weird things if they are lacking a
small bypass capacitor. Higher speed digital circuits will also often misbehave
without small capacitors on each chip.
Inductors can also be used to filter off power supply noise. Inductors are
placed in series in the power supply line. At low frequencies, they are
essentially a short circuit, allowing all of the DC power to go through the
line. At higher frequencies, the reactance starts to climb (remember Xl=jwL, so
Xl is bigger when w is bigger). This presents a higher impedence to the noise
source, and less noise current flows. Inductors are often called chokes when
they are used this way.
Capacitors and inductors are very often used in filter circuits. Circuits can
be made which pass or reject only high or only low frequencies, or perhaps let
only a particular frequency band through. Because of the complexity of this
subject, filters are discussed in more detail in a seperate article.
As was previously mentioned, capacitors and inductors may be used to balance
out reactance on a line, as is often done with power lines.
One neat trick is to use a capacitor to drop voltage from an AC power line.
This is sometimes done in places where a heavy transformer is undesirable.
However, it has all of the pitfalls of using a resistor to drop voltage in a
circuit. First, the actual voltage dropped varies, depending on the current that
is flowing. This means that this technique is only good when a constant amount
of current is flowing. Second, because a transformer is not used, there is no
isolation from the main AC line. This technique also has a benefit that no heat
is generated, unlike a resistor.
Note that a diode and a capacitor can be used as an AM demodulating circuit.
The diode rectifies the signal, and the capacitor filters off the higher
frequency carrier. This is important, because diodes and capacitors used for
other purposes will sometimes make a perfect AM receiver in the middle of your
circuit.
A little bit of variation
Sometimes it is valuable to have a variable capacitor or a variable inductor.
In a radio receiver, for example, the receiving frequency might depend on the
resonnant frequency of a particular RLC circuit (a circuit with a resistor,
capacitor, and inductor - see the article on filters for more details). By
varying the capacitance, you can vary the frequency that the radio receives.
Older stereos and televisions used this principle. The stereo would have a dial,
which was usually connected to a variable capacitor (usually by a long string
and pulley system). The capacitor was constructed by simply using alternating
plates, one set being stationary and the other movable. By varying the spacing
of the plates, the capacitance was varied. Older television dials did the same
thing, but had fixed plate spacing depending on the channel selected, instead of
being completely tunable like stereos.
Variable inductors are also common. These are sometimes made by using a
conductor wiper, similar to how variable resistors are constructed, and
sometimes are made by using a variable core inside the inductor.
Variable capacitors and inductors will be specified by their range, in
addition to the normal capacitor and inductor specs (max voltage, max current,
etc).
 This
vector has a magnitude and a direction. The magnitude is the square root of R
squared plus X squared (where R and X are the real and imaginary parts), and the
angle, usually written as a greek theta, is the inverse tangent of (X/R). We
write this as (magnitude)<(angle), where the < is really an angle sign. If
you are writing it by hand, you make it look more like an angle than a less than
sign. Some people continue the bottom of the line under the angle value, so that
it cannot be mistaken for a less than sign.
This
vector has a magnitude and a direction. The magnitude is the square root of R
squared plus X squared (where R and X are the real and imaginary parts), and the
angle, usually written as a greek theta, is the inverse tangent of (X/R). We
write this as (magnitude)<(angle), where the < is really an angle sign. If
you are writing it by hand, you make it look more like an angle than a less than
sign. Some people continue the bottom of the line under the angle value, so that
it cannot be mistaken for a less than sign.
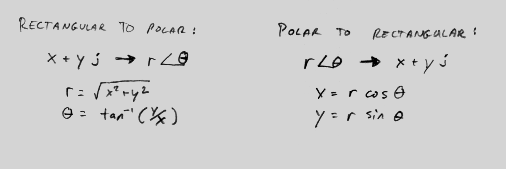 To multiply two phasors together (in polar form), multiply the magnetudes and
add the angles. To divide, divide the magnitude and subtract the angles.
Addition and subtraction are more easily done in rectangular form. Just
add/subtract all of the real terms as neccessary, and then add/subtract all of
the imaginary terms.
To multiply two phasors together (in polar form), multiply the magnetudes and
add the angles. To divide, divide the magnitude and subtract the angles.
Addition and subtraction are more easily done in rectangular form. Just
add/subtract all of the real terms as neccessary, and then add/subtract all of
the imaginary terms.