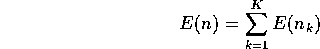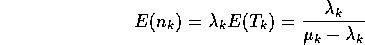-
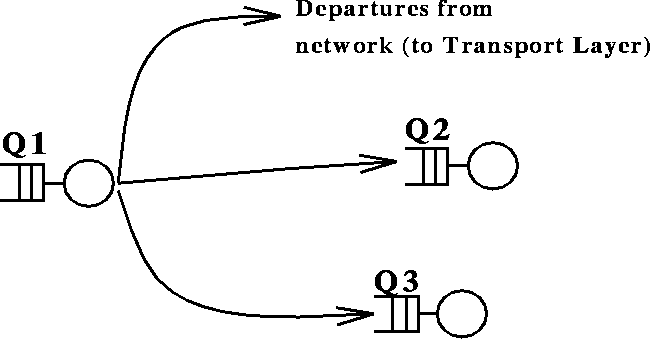
To the input of Q2 with probability
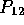 ,
, -
To the input of Q3 with probability
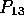 ,
, -
Or leaves the network with probability
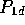 .
.
 ,
and leaves the network with probability
,
and leaves the network with probability
 .
.
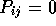 .
.

where K is the number of queues in the network.
-
The servers in each of the K queues are independent of each other
and have rates
 .
. -
The external arrivals (if any) at each queue are independent
Poisson processes with rates
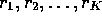 (
(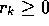 for
for
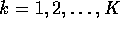 ).
). -
The network uses random routing.

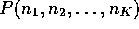 =
probability of (
=
probability of (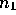 packets in Q1,
packets in Q1, 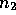 packets in Q2, ...,
packets in Q2, ...,
 packets in QK), then
packets in QK), then
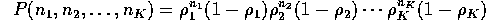
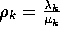 and
and 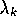 = total arrival
rate of all packets to Qk for k = 1, 2, ..., K.
= total arrival
rate of all packets to Qk for k = 1, 2, ..., K.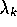 = total arrival rate to Qk.
= total arrival rate to Qk.
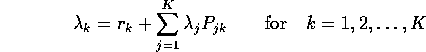
 if
if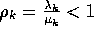 for
for
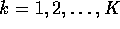 , and
, and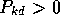 ), or
), or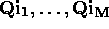 , such that
, such that
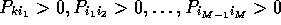 and
and
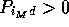 .
.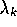 's and
the
's and
the 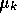 's and we know each
Qk is an M/M/1 queue, so we can find the mean delay a packet experiences
in Qk:
's and we know each
Qk is an M/M/1 queue, so we can find the mean delay a packet experiences
in Qk:
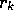 is the rate at which
new packets enter the network at Qk and all queues are stable
(
is the rate at which
new packets enter the network at Qk and all queues are stable
(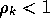 ), then the
total network throughput is
), then the
total network throughput is