|
|
||||||||||||||||||||||||||||||||
The Component Method, Part 2 |
|||||||||||||||||||||||||||||||||
| Summing the Components
Now that we have replaced all the bad vector with good vectors, we have a much simpler system of vectors to sum. (But remember, this system of good vectors is equivalent in every way with the system of bad vectors we started with.) We can now begin to add the good vectors. Since vectors are easiest to sum when they point along the same line (parallel or anti-parallel) we will add those vectors first. There are two sets of such vectors -- those that point along the x-direction (the horizontal line), and those that point along the y-direction (the vertical line). You will probably find it convenient, especially when summing many vectors, to create a table that sorts the good vectors according to direction. At this point it will be easiest to refer to an example:
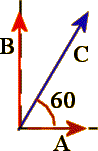
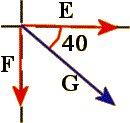
In the figure above, we are given two vectors, C and G, to sum. For each vector we draw an x-axis and y-axis. For vector C, the corresponding good vectors are denoted A and B and are shown in the following figure. Notice that we also show the good vectors for vector G, which we call E and F. The length (magnitude) of vector A is given by A = C X COS(60) = 10 X (0.500) = 5.00, and for vector B, B = C XSIN(60) = 10 X (.867) = 8.67. For vector G we do the same: E = G X COS(40) = 8 X (0.766) = 6.13, F = G X SIN(40) = 8 X (0.643) = 5.14.
Now that we have nothing left but good vectors, we place them in a table according to direction.
The following is the same table, but with the lengths of the vectors substituted for the symbols. Notice the sign convention: We use negative to denote vectors that point to the left or down.
Now we take advantage of the fact that parallel vectors are easy to add. Those vectors listed in the x-direction column (A and E) point along the same direction, so we just add their respective lengths and put that total at the bottom of the column. We do the same for the y-direction for vectors B and F.
These vector sums at the bottom of each column are, naturally, vectors. Essentially, we have reduced our problem of summing two bad vectors (C and G) to a problem of summing two perpendicular vectors (X and Y):
In summary, vectors X and Y are also easy to add because they are perpendicular to each other. |
|||||||||||||||||||||||||||||||||
| The Finale: Summing the
Perpendicular Vectors The two vectors X and Y above are shown in the following figure. Notice that they form a rectangle, with two sides of the rectangle forming a right triangle, and that these two vectors sum to form a resultant vector R. In other words, R = X + Y.
This resultant vector forms the hypotenuse of the triangle, so its length is simply given by the Pythagorean Theorem, R2 = X2 + Y2.
So in our example the length of our resultant vector is found from R2 = (2.54)2 + (10.14)2 = 6.45 + 102.82 = 109.27 Therefore, R = 10.45. Finding the direction of R is a little trickier, and requires the use of the arctangent button on your calculator. Here is the expression, where we use the greek symbol q to denote the direction: q = ARCTAN(Y/X). In our example, q is given by q = ARCTAN(2.54/10.14) = 14.0 degrees. Which angle do we get? Whichever vector is in the denominator (bottom half of the fraction) is the reference vector for the angle. In other words, the resultant vector R is 14.0 degrees with respect to the direction defined along vector X.
Once you have found the length and direction of the resultant vector, you are finished! |
|||||||||||||||||||||||||||||||||
So now what? Finally, if you think you have followed this discussion, test your ability.
|
|||||||||||||||||||||||||||||||||
  |
|||||||||||||||||||||||||||||||||
