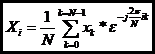The Discrete Fourier Transform (DFT)

Introduction

Here we will start with the Fourier series of a band-limited, periodic function and see what happens when it is sampled using Ideal sampling. The result will be the Discrete Fourier Transform (DFT). We can then understand the characteristics of periodic, discrete-time signals in the frequency domain.

The Periodic Signal

Assume x(t) is a band-limited, periodic function with maximum frequency W and period T. Its complex exponential series can then be written as:

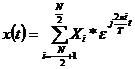
Where N/2 ≥ WT is sufficient to cover all the non-zero coefficients (those with low enough energy to be approximated away) and:

The Fourier Transform, X(jw), of x(t) is then a finite sum of d-functions and can be sketched as a function of frequency.

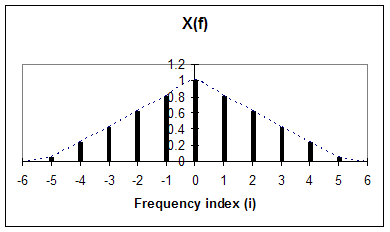
Sampling x(t)

If we now sample (we shall assume Ideal sampling to simplify the derivation) x(t) at the Nyquist rate of 2W, the spectrum becomes periodic as was determined in the discussion on sampling. The spectrum also gets a gain factor (not discussed earlier) which is introduced in the sampling process.

Assume that we sample f(t) ideally over the time interval (0, a) with n samples.

Integrating (using the sifting property of d-functions)

But

So the sampled function is N/a time stronger than the original. We can adjust for this by scaling the impulse train by T/M in our development.

And

Where M is the largest integer that corresponds to a frequency that is less than 2TW at the selected sampling rate.

The Fourier series for the discrete-time signal is then

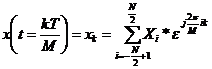
Or, if we sample at exactly the Nyquist rate, M=N and

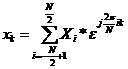
Or Since the X_i are periodic with period N

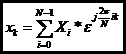
Which is one half of the two DFT equations

The second half of the DFT is obtained by starting with

We can now substitute the sampling sum of d-functions for x(t,T)

Interchanging the order of integration and summation and again using the sifting property of d-functions yields the second half of the DFT pair

Often these two equations are simplified by assuming that

Resulting in the DFT transform pair

Direct DFT
Inverse DFT

It should be noted that the 1/N factor is sometimes placed in the Inverse DFT equation. This can be a source of confusion.

DFT: The Matrix Formulation

The equations above can be restated as a pair of matrix equations. Let

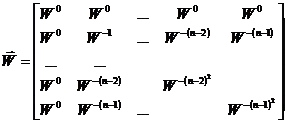then, it’s inverse is

Now define 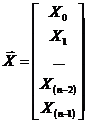and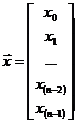

The DFT transform pair is then given by the matrix equations

and