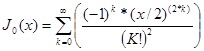Generalized Fourier Series

Definitions

1.

0

Ai (¹ 0 or ¥) if i = j

A set of functions {F_i(t)} is said to be orthogonal over an interval [a,b] iff

2. A set of functions is said to be complete over an interval [a,b] if any waveform with a finite number of discontinuities on [a,b] can be expressed as a linear combination of members of that set.

Theorem: The Fourier Series

Given: {F_i(t)} is a complete, orthogonal set on [a,b],
, and
f(t) has a finite number of discontinuities on [a,b].

Then: over [a,b]

Where: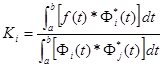

Proof:

Since {F_i(t)} is a complete set on [a,b]

over [a,b]

Multiplying both sides of the equation by yields

Now integrating both sides over [a,b]

Reversing the order of integration and summation (linear operators) and moving the constants out of the integral leaves

But 0 for i ¹ j so we are left with only the i^th term of the sum

Solving for K_i

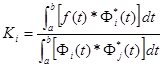
Q. E. D.

Examples of Complete, Orthogonal Sets

{Fi(t)}	[a,b]
{ 1, sin(nw0t), cos(nw0t) } ( 1 ³ n ³ ¥ )	[ -T/2, T/2] ( T = 2p/w0 )
{ exp(jnw0t) } ( - ¥ ³ n ³ ¥ )	[ -T/2, T/2] ( T = 2p/w0 )
Pn(t) – The Legendre Polynomials P0(t) = 1 P1(t)= t P2(t)= ½( 3t^2 – 1) P3(t)= ½( 5t^3 – 3t) …	[ -1, 1 ]
- The 0^th Order Bessel Function rn is the nth root of J0(t) = 0 r0 = 2.41, r1 = 5.51, r2 = 8.64, r3 = 11.79, …	[0, a]

Example: The Sawtooth or Sweep function

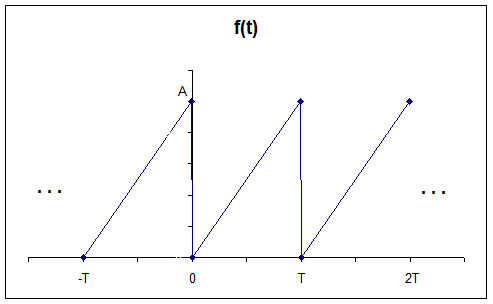
f(t) = (A/T)*t

t in [0, T)

Use { 1, sin(nw₀t), cos(nw₀t) } (w₀ = 2*p/T)

0

0

First find a₀

note: the second and third integrals are zero since the area under a sine or cosine over a integer number of cycles is always zero. They have equal areas above and below the axis.

Solving for a₀

a₀ = A/2 Note: This is the average or DC value of the waveform

Now find b_n for n ³ 1

again

Now multiply both sides by and integrate over the interval

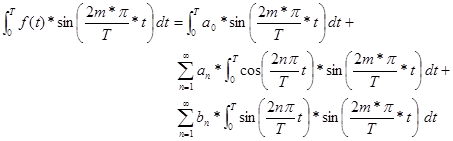
The first integral is zero as before; the second is also zero since

HW: check it out

The third integral uses another trigonometric identity

The (x+y) terms again all yield zero and all of the (x-y) terms are also zero except for the one where m=n. This yields

But cos(0) = 1 and the integral becomes T and we have

or

Integrating this requires the use of integration by parts

We want to get rid of the t in the integral so let u = t and dv be the rest. This yields

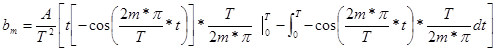
The integral is once again zero for the usual reason. The first term becomes

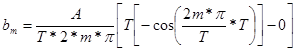
Simplifying further

or

HW: Show that the a_n are all zero for n ¹ 0

The Complex Exponential Series: Another form of the Sine-Cosine Series

Euler’s Formula

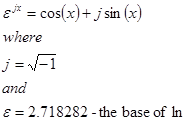
This also means that

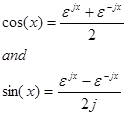
The unit circle represents exp(x) as a unit vector of magnitude 1 and angle q

sin(x)

cos(x)

1

q

The complex exponential is therefore closely related to the Phasor analysis used in AC circuits and

HW: find the complex exponential form for the Fourier Series of the sawtooth example function.

Note: the answer should be consistent with

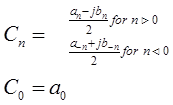
Note: Both the Sine-Cosine and Complex Exponential sets consist of members that are periodic functions. Each of their members has a frequency, which is a multiple of the fundamental frequency that has a period, T, equal to the length of the region of orthogonality. Each element is also periodic with period T and therefore their sum is also periodic.

Although we made no general statement in the theory about the behavior of the original function outside of the region of orthogonality, the Fourier series will only represent a periodic function. It, however, will represent a periodic function over all time.

Further note: at discontinuities, there will be some residual error